

Which is the kernel of the Fourier integral. Remember, our corkscrew function is:īut when it is not rotating, ω = 0, and when it has unity modulus, A = 1, we just get left with At any particular value of K (proportional, physically, to the scattering angle θ), we calculate the Fourier transform (Fraunhofer diffraction) amplitude by multiplying f(x) by a non-rotating corkscrew function of periodicity K and modulus (radius) of unity, and adding up (integrating) the value of the resulting function over all space. I’ve used a capital K, for reasons which will become clearer later. I’m using the very simplest definition of the Fourier transform so that we don’t get caught up with factors of 2π, minus signs or anything to do with the wavelength. Now lets think about doing the Fourier transform of our grating explicitly, using the Fourier transform integral This is the reciprocal relationship between the real space grating spacing and the spacing of peaks in reciprocal space. Obviously, for constant λ the values of θ where strong interference occurs has to increase if the grating spacing Δx gets smaller. We see that this occurs when Nλ=Δx sin θ, which is the famous diffraction grating equation. The diffraction maxima occur when the path difference between adjacent phase threads, subtending from each grating, is exactly Nλ, where N is an integer. When the gratings in ‘real space’ get closer and closer, the diffraction orders in ‘reciprocal space’ get wider and wider: that is, they occur at higher and higher scattering angles. In the case of the diffraction grating, this ‘reciprocal’ relationship is very easy to understand. The reason for this is that any prevalent distance, say Δx (such as the distance between atoms or gratings) in ‘real’ space (that is, at the object function which is doing the scattering), expresses itself as a distance 1/Δx in the Fourier domain. We call the space of the Fourier domain ‘reciprocal space’.

If we are thinking of the Fourier transform as the amplitude in the Fraunhofer diffraction pattern, then these spikes are the usual diffraction orders that arise from an optical grating.
#Diffraction gradient series#
Then its Fourier transform is also a one-dimensional series of spikes. When we have an infinitely large one-dimensional grating, of the functional form: On this page, I want to think about it in an alternative way, so that when we come to think of three-dimensional scattering and crystallography, we will have intuitive way of constructing the reciprocal lattice. We’ve already worked out the Fourier transform of diffraction grating on the previous page.
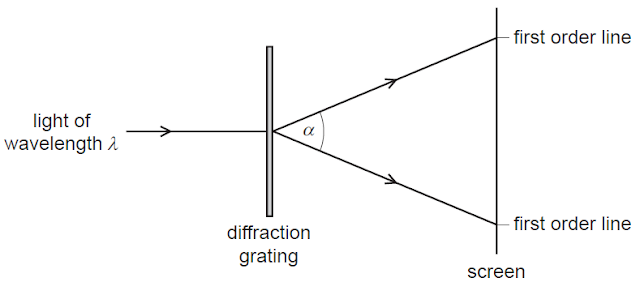
The Fourier transform of a diffraction grating


 0 kommentar(er)
0 kommentar(er)
